ACool & Blog

前言

最近一段时间一直在刷Leetcode，目前AC数不算多，地址见此 https://github.com/starFalll/LeetCode 。前几个月刷完了《剑指offer》的60多道题，地址在此 https://github.com/starFalll/Sword-pointing-to-offer ，可惜当初刷题之时，忘了加上题解，不过大多数题可以参考 牛客网 的讨论区。Leetcode里面目前我觉得最有意思的是操作系统中的页面置换算法LRU/LFU 的实现。

页面置换算法

LRU算法及实现

LRU(Least recently used) 中文名为最近最久未使用算法，维基百科地址见此，即当存储不够时，需要置换页面，LRU 算法则是将最进最久未使用过的页面换出，再将新页面换入。如图所示：

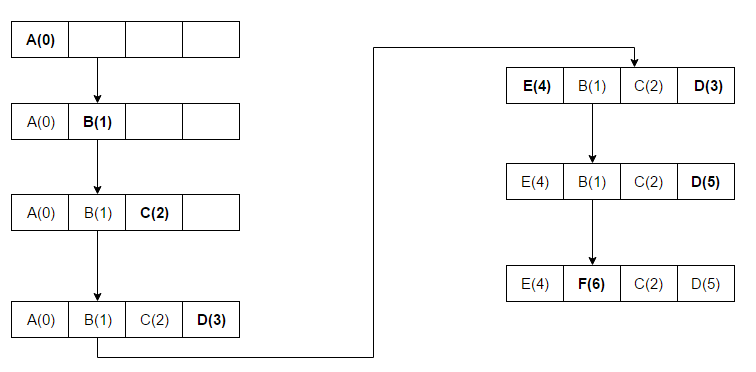
在上面的例子中，ABCD页被放在具有序列号的块中（每个新的页面增加1），当访问E时，它不在缓存中，所以需要换入缓存中的一个块。但是此时缓存已经没有多余的块了，根据LRU算法，由于A具有最低的序列号（A（0）），E将取代A。

下面来看看Leetcode的题干：

Design and implement a data structure for Least Recently Used (LRU) cache. It should support the following operations: get and put.

get(key) - Get the value (will always be positive) of the key if the key exists in the cache, otherwise return -1. put(key, value) - Set or insert the value if the key is not already present. When the cache reached its capacity, it should invalidate the least recently used item before inserting a new item.

Follow up: Could you do both operations in O(1) time complexity?

Example:

LRUCache cache = new LRUCache( 2 / capacity / );

cache.put(1, 1);

cache.put(2, 2);

cache.get(1); // returns 1

cache.put(3, 3); // evicts key 2

cache.get(2); // returns -1 (not found)

cache.put(4, 4); // evicts key 1

cache.get(1); // returns -1 (not found)

cache.get(3); // returns 3

cache.get(4); // returns 4

我们来分析一下，题目要求 put 和 get 操作都能在 O(1) 时间内完成，因为 get 具有查找操作，put 具有插入和删除的操作，所以查找，插入和删除操作必须要在 O(1) 时间内完成。所以我们可以使用一个双向链表和一个 HashMap ，因为：

双向链表能够在O(1)时间内添加和删除节点，单链表则不行
HashMap 保存每个节点的地址，可以基本保证在O(1)时间内查找节点

有了相关的数据结构，具体如何实现呢？如何判断哪个页面是最近最久未使用的呢？

我们可以在每次访问时，将所访问页面换到链表头部，这样，越靠近链表头部，表示节点上次访问距离现在时间最短，尾部的节点表示最近访问最少。

对于 get 操作：

访问节点时，如果节点存在，把该节点交换到链表头部，同时更新hash表中该节点的地址。

对于 put 操作：插入节点时，如果 cache 的 size 达到了上限，则删除尾部节点，同时要在hash表中删除对应的项，最后将新节点插入链表头部；如果 cahce 的 size 没有达到上限，则只需要将新节点插入链表头部。

双向链表如何实现？

C++的std::list 就是个双向链表，且它有个 splice()方法，O(1)时间，非常好用。

具体代码如下：

//C++
class LRUCache {
private:
    struct CacheNode{
        int key;
        int value;
        CacheNode(int k,int v):key(k),value(v){}
    };
    list<CacheNode> cacheList;
    unordered_map<int,list<CacheNode>::iterator> cacheMap;
    int _capacity;
public:
    LRUCache(int capacity) {
        this->_capacity=capacity;
    }

    int get(int key) {
        if(cacheMap.find(key)==cacheMap.end()) return -1;
        //put node to list head and update map
        cacheList.splice(cacheList.begin(),cacheList,cacheMap[key]);
        cacheMap[key]=cacheList.begin();
        return cacheMap[key]->value;
    }

    void put(int key, int value) {
        if(cacheMap.find(key)==cacheMap.end()){
            if(cacheList.size()==_capacity){
                cacheMap.erase(cacheList.back().key);
                cacheList.pop_back();
            }
            cacheList.push_front(CacheNode(key,value));
            cacheMap[key]=cacheList.begin();
        }
        else{
            cacheMap[key]->value=value;
            cacheList.splice(cacheList.begin(),cacheList,cacheMap[key]);
            cacheMap[key]=cacheList.begin();
        }
    }
};

LFU 算法及实现

LFU(Least Frequently Used) 中文名为最少使用算法，维基百科地址见此。和 LRU 算法类似，当缓存已满并需要更多空间时，将使用频率最低的页面换出，将新的页面换入。如图所示：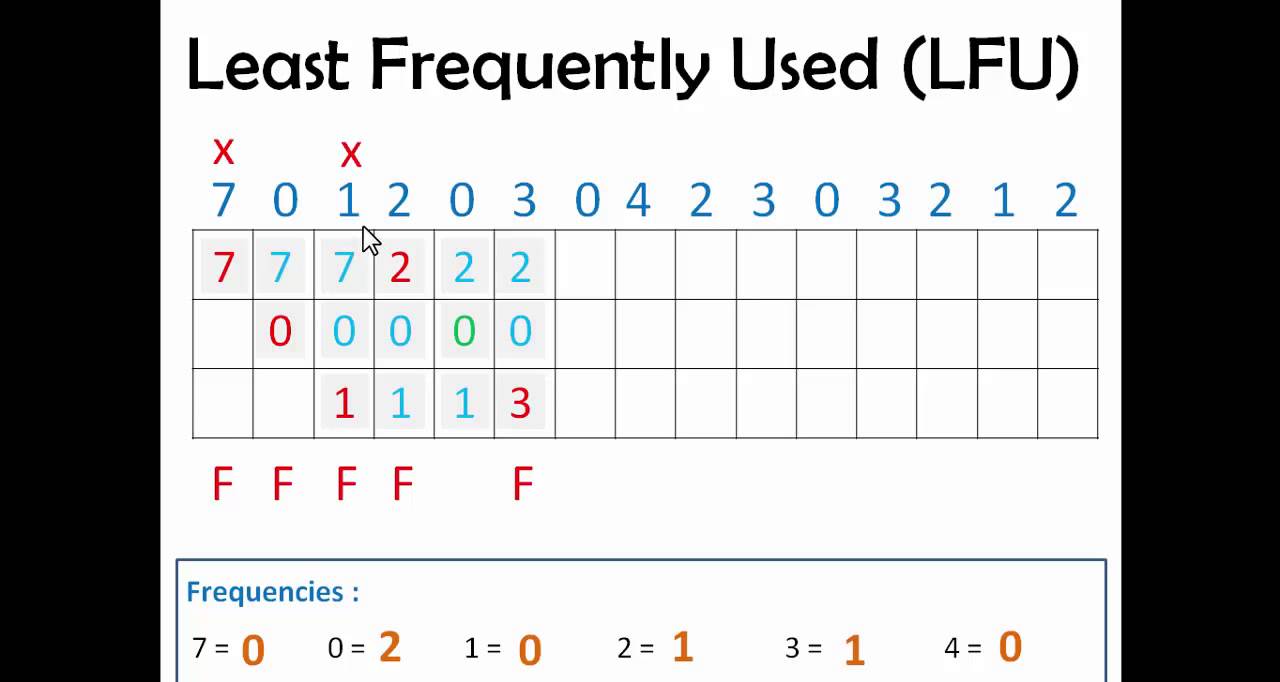

在上面的例子中，当换入页面3的时候，因为0页面访问了2次，而1页面只访问了一次，所以换出1页面。

LRU算法是首先淘汰最长时间未被使用的页面，而LFU是先淘汰一定时间内被访问次数最少的页面，一定时间内被访问次数最少的页面不一定是长时间未被使用的页面，这是两种算法主要的区别。举个例子，比如说我们的cache的大小为3，然后我们按顺序存入 6，5，6，5，6，9，这时候cache刚好被装满了（5，6，9），因为put进去之前存在的数不会占用额外地方。那么此时我们想再put进去一个7，如果使用LRU算法，应该将 5 删除，因为 5 最久未被使用，而如果使用LFU算法，则应该删除 9，因为 9 被使用的次数最少，只使用了一次。相信这个简单的例子可以大概说明二者的区别。

下面来看看Leetcode的题干：

Design and implement a data structure for Least Frequently Used (LFU) cache. It should support the following operations: get and put.

get(key) - Get the value (will always be positive) of the key if the key exists in the cache, otherwise return -1. put(key, value) - Set or insert the value if the key is not already present. When the cache reaches its capacity, it should invalidate the least frequently used item before inserting a new item. For the purpose of this problem, when there is a tie (i.e., two or more keys that have the same frequency), the least recently used key would be evicted.

Follow up: Could you do both operations in O(1) time complexity?

Example:

LFUCache cache = new LFUCache( 2 / capacity / );

cache.put(1, 1);

cache.put(2, 2);

cache.get(1); // returns 1

cache.put(3, 3); // evicts key 2

cache.get(2); // returns -1 (not found)

cache.get(3); // returns 3.

cache.put(4, 4); // evicts key 1.

cache.get(1); // returns -1 (not found)

cache.get(3); // returns 3

cache.get(4); // returns 4

这道题比LRU要更难一点，因为之前的LRU只需要将数字按照顺序存入 list ，list 末尾的页面总算满足 LRU 的，但是这道题不同，进入的顺序并不完全能决定换出的页面，还需要统计每个页面被访问的次数。

首先可以想到使用 HashMap 保存页面及其被访问次数的映射，为了方便操作，我们可以：

将相同频率的页面都放到一个 list 中
由1则需要另一个哈希表 freq 来建立频率和一个里面所有页面都是当前频率的 list 之间的映射
又因为操作要在 O(1)的时间内完成，所以再用一个哈希表 iter 来建立页面和 freq 中页面的位置之间的映射
两个变量cap 和 minFreq，分别来保存cache的大小和当前最小的频率

所以可以建立如下数据结构：

int _cap;
int minfrq;
unordered_map<int,pair<int,int>> m;//key to {value,freq}
unordered_map<int,list<int>::iterator> miter;//key to list iterator
unordered_map<int,list<int>> mfrq;//freq to key list

为了更好的讲解思路，我们还是用例子来说明吧，我们假设 cache 的大小为2，假设我们已经按顺序put进去5，4，那么来看一下内部的数据是怎么保存的，由于 value 的值并不是很重要，为了不影响 key 和 frequence ，我们采用 value# 来标记：

5 -> {value5, 1}

4 -> {value4, 1}

freq:

1 -> {5，4}

iter:

4 -> list.begin() + 1

5 -> list.begin()

这应该不是很难理解，m 中 5 对应的频率为 1，4 对应的频率为 1，然后 freq 中频率为 1 的有 4 和 5。iter 中是 key 所在freq 中对应链表中的位置的 iterator。然后我们的下一步操作是 get(5)，下面是get需要做的步骤：

如果m中不存在5，那么返回-1
从freq中频率为1的list中将5删除
将m中5对应的frequence值自增1
将5保存到freq中频率为2的list的末尾
在iter中保存5在freq中频率为2的list中的位置
如果freq中频率为minFreq的list为空，minFreq自增1
返回m中5对应的value值

经过这些步骤后，我们再来看下此时内部数据的值：

5 -> {value5, 2}

4 -> {value4, 1}

freq:

1 -> {4}

2 -> {5}

iter:

4 -> list.begin()

5 -> list.begin()

这应该不是很难理解，m 中 5 对应的频率为 2，4 对应的频率为 1，然后 freq 中频率为 1 的只有 4，频率为 2 的只有 5。iter 中是 key 所在 freq 中对应链表中的位置的 iterator。然后我们下一步操作是要 put(7)，下面是put需要做的步骤：

如果调用get(7)返回的结果不是-1，那么在将m中7对应的value更新为当前value，并返回
如果此时m的大小大于了cap，即超过了cache的容量，则：

a）在m中移除minFreq对应的list的首元素的纪录，即移除4 -> {value4, 1}

b）在iter中清除4对应的纪录，即移除4 -> list.begin()

c）在freq中移除minFreq对应的list的首元素，即移除4

在m中建立7的映射，即 7 -> {value7, 1}
在freq中频率为1的list末尾加上7
在iter中保存7在freq中频率为1的list中的位置
minFreq重置为1

经过这些步骤后，我们再来看下此时内部数据的值：

5 -> {value5, 2}

7 -> {value7, 1}

freq:

1 -> {7}

2 -> {5}

iter:

7 -> list.begin()

5 -> list.begin()

代码如下：

//c++
class LFUCache {
private:
    int _cap;
    int minfrq;
    unordered_map<int,pair<int,int>> m;//key to {value,freq}
    unordered_map<int,list<int>::iterator> miter;//key to list iterator
    unordered_map<int,list<int>> mfrq;//freq to key list
public:
    LFUCache(int capacity) {
        _cap=capacity;
    }

    int get(int key) {
        if(m.count(key)==0) return -1;
        //change key's freq add 1,and move key's position
        mfrq[m[key].second].erase(miter[key]);
        m[key].second++;
        mfrq[m[key].second].push_back(key);
        miter[key]=--mfrq[m[key].second].end();
        if(mfrq[minfrq].size()==0)
            minfrq++;
        return m[key].first;
    }

    void put(int key, int value) {
        if(_cap<=0) return;
        int find=get(key);
        if(find!=-1){
            m[key].first=value;
            //there were already move key's position in get operation
            return;
        }
        if(m.size()==_cap){//remove minfrq key
            m.erase(mfrq[minfrq].front());
            miter.erase(mfrq[minfrq].front());
            mfrq[minfrq].pop_front();
        }
        m[key]={value,1};
        mfrq[1].push_back(key);
        miter[key]=--mfrq[1].end();
        minfrq=1;
    }
};